Counters, Idempotence And Forgetful Bloom Filters
One of the papers that’s grabbed my attention recently is “Idempotent Distributed Counters using a Forgetful Bloom Filter” by Rajath Subramanyam et. al. In it, the authors tackle a surprisingly tricky problem: how do you make distributed counters more accurate?
Over the next couple of posts, we’ll be taking a look at their approach.
Counters on an unreliable network
Counters, from polls & like buttons to page-views & play-counts, are everywhere on the web.
In most cases, they’re implemented as a number (stored on the server-side), coupled with increment and decrement operations that clients can access by sending a +1 or -1 messages. In this post, we’ll be addressing how a single server with multiple clients behaves.
The authors show how inaccuracy can creep unheralded into these counters:
When a client sends an operation to the server, the server might fail after applying the operation but before sending back an ack[nowledgement]. In this case, the client has no way to know whether the operation was applied or not.
The same situation occurs when the server is healthy, but the network is dropping or delaying messages - so it’s not enough to write a fault-free service.
In this scenario, sending a duplicate request might lead to an over-count, whereas not sending one might lead to an under-count if there was indeed a server failure.
If counter accuracy matters, we may well want to deal with this ambiguity. But how?
The approaches the paper discusses involve tagging each operation with a unique identifier. If the client retries an operation, they re-send the same unique id. The authors suggest a tuple of <client-id, sequence-number>, which they call a timestamp.
The aim is to make the +1 and -1 operations idempotent by tracking the timestamp of the operations that the server has already processed and rejecting duplicates. Once operations are idempotent, clients can retry without fear of an operation being processed multiple times.
Keeping a total history of operations…
The paper references previous attempts to solve this problem by keeping a total history of all timestamps.
… in a set
If the server keeps a simple set of all timestamps it has seen, it can reject retries of those operations by checking if the timestamp is already a member of the set.
This approach is rarely practical, because it becomes:
very costly in the long run – the history of operations can grow unboundedly and checking for duplicates becomes prohibitively expensive.
… in Bloom filter
Using Bloom Filter - which represent a set of any number of members with a fixed amount of memory and support constant-time membership checks - addresses some of issues with a simple set.
Bloom filters achieve their constant size by offering probablistic membership checks - prone to false positives. Worryingly, their false positive probability (FPP) increases with use:
As the number of elements inserted into a Bloom filter increases, so does the probability of a false positive (i.e., membership checks may erroneously return true). False positives result in an under-count.
Bloom filters don’t support deleting or retiring members from the set, so there’s no way to combat this deterioration. Eventually, a Bloom filter will respond to every membership check with true, whether it contains the item or not.
Forgetful Bloom Filters (FBFs) - keeping a partial history
Subramanyam et. al.’s proposed approach takes advantage of the observation that:
Storing old updates becomes less valuable over time as these operations become increasingly unlikely to be retried. In fact, clients often have write request timeout beyond which they give up on the write.
The conjecture of the authors is that the server only needs to remember a moving window of history, so long as that window is longer than the period the client will keep re-trying the operation in.
To achieve this, the authors propose a new suite of data-structures - Forgetful Bloom Filters (FBFs) - which are based on the Bloom filters we introduced in the last section.
Like a traditional Bloom filter, an FBF supports an element addition operation that is idempotent. An FBF allows insertion and membership-checking of items with the same asymptotic cost as a Bloom filter …. Like the traditional Bloom filter, false positives can occur in the FBF, thus leading to an under-count for counters.
Instead of avoiding false positives entirely, the aim is to keep the FPP acceptably low. As the name suggests, a Forgetful Bloom Filter keeps the total number of members in check by forgetting old members.
an FBF automatically expires older items (the timeout period can be adjusted).
Under the hood, an FBF comprises of several Bloom filters:
An FBF does so by using multiple constituent Bloom filters to essentially maintain a moving window of recent operations.
The Basic FBF is the easiest variation to understand:
In its simplest form, an FBF contains three Bloom filters:
- a future Bloom filter,
- a present Bloom filter, and
- a past Bloom filter.
Inserting a member into an FBF is simply a matter of inserting it into the future and present Bloom filters.
Checking for membership in an FBF is the same as checking for membership in any one of its constituent Bloom filters - although the authors also introduce an optimisation that lowers the FPP even further.
To maintain a moving time window, an FBF also has a periodic refresh operation applied to it:
the following operations are performed atomically:
- The past Bloom filter is dropped;
- The current present Bloom filter is turned into the new past Bloom filter;
- The current future Bloom filter is turned into the new present Bloom filter;
- A new, empty future Bloom filter is added to the FBF.
This way, we know that any item added to the FBF will be forgotten within three refreshes - creating the moving window described before.
Evaluation
Using a Basic FPF for filtering out duplicate operations has some attractive qualities. Membership checks take constant time, and the data-structure consumes constant space.
Eagle-eyed readers will have noticed that nothing in this section of the paper are specific to counters - and could be applied to make retries of any non-idempotent operation safer.
There are some open issues with using them, however:
Inconsistent network latency
In the paper, the authors advise setting the FBF refresh interval to be:
greater than the counter write request timeout period …, beyond which the client will stop retrying the update operation. This ensures that the FBF captures all relevant operations, and that older forgotten operations will not be retried by clients.
It appears that insight holds only if the network latency between the client and server is constant. If the network latency increases during the period in which the client is retrying, some retries might arrive at the server after the window.
For instance, the client write timeout might be 10 seconds, and the latency might begin at 1 second, eventually increasing to 5. If the first operation is sent at t1, the server will receive it at t1 + 1. The last request from the client will be at t1 + 10, and will be received at t1 + 10 + 5. In this scenario, all the clients’ retries will be within 10 seconds, but the server will see retries spanning a 14 second window.
The question becomes: “How much history should the server keep in their window?”
FPP increases with load
Because the refresh period is constant, the more load the server receives, the higher the FPP. The authors’ empirical evaluation of a Basic FBF confirms this:
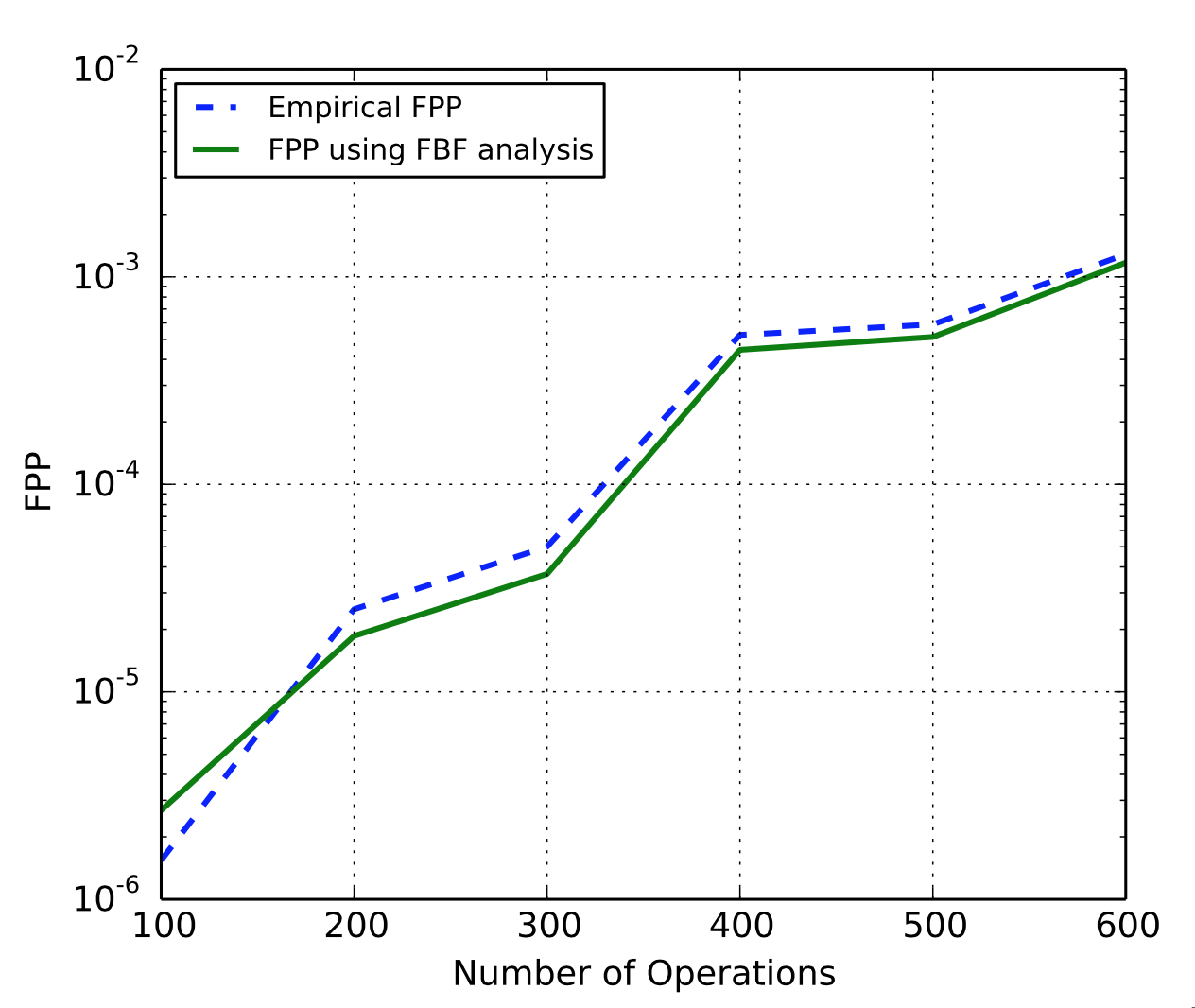
Fig. 9: False Positive Probability(FPP) of an FBF comparison with the empirical FPP.
In the next post, we’ll be looking at the author’s Adaptive N-BFBs, which aim to guarantee a maximum bound on the filter’s FPP.